Being an impatient person, I've always tried to make my 'code' run faster. In my experience, in most ML algorithms the 'core' bottleneck in computation seems to be one of the following
- (Dense/Sparse) Matrix - Vector product
- (Dense/Sparse) Matrix - Dense Matrix product
For example, consider any binary classification or regression task with N examples and dimension P. The computational bottleneck (for training and testing) is the product of the data matrix X [NxP] (sparse or dense depending on the data) and the parameter vector w [Px1]. In any multi-class classification task with K classes, the bottleneck is the product of X and the parameter matrix W [PxK].
Even in completely unsupervised settings such as clustering, we need to invariably either compute a distance measure between the data points and the cluster means or calculate some sufficient statistics from the data. In most cases, this can be written efficiently in terms of a matrix products. I give two examples - (a) Kmeans and (b) Multinomial Mixtures.
For kmeans, the cluster means is denoted by M [PxK], where K is the number of clusters. The distance matrix D [NxK] is the euclidean distance between each row in X and each column in M. To compute D,
D = ((X∘X)eD)eKT - 2 XxM + eK((M∘M)eD)
where ed denotes a vector of ones with dimension [dx1]. The expressions on the right and left of the RHS can be computed efficiently in O(NxP) and O(PxK), but the computation of the term in the middle is O(NxPxK) which is the bottleneck. In Multinomial Mixture, instead of the cluster means we have class-probabilities in matrix M. In this case, the distance measure is simply the log-probability of the instance given a class i.e. Xxlog(M) which is again matrix product.
So, how do we make ML implementations faster? Matrix multiplication seems like it should be a very well studied topic and all that remains is to choose an efficient matrix multiplication library and plug it in. Unfortunately, 'choosing' the right library turned out to be a much harder problem than I thought. There are tons of implementations of the BLAS interface and each has a different implementation of the matrix multiplication function (see DGEMM function).
I performed a series of dense-dense matrix multiplication experiments on 5 BLAS implementations - ATLAS, EIGEN matrix template library, Intel's Math Kernel Library (MKL), OpenBLAS, and AMD's core Math Library (ACML) so that I could choose the 'right' library. Note that MATLAB internally uses Intel's MKL library although with some overhead.
All the tests were performed on 48 core and 66GB RAM machine with configuration given here.
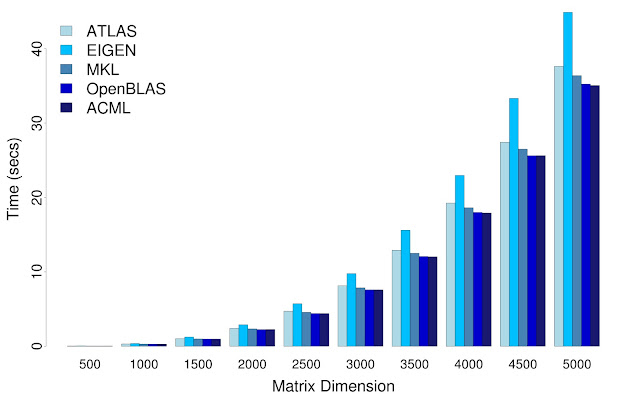
I performed a sequence of matrix multiplications on squared matrices with increasingly larger dimensions. The time-taken for each BLAS implementation is reported (averaged over 5 runs) is shown below,
where ed denotes a vector of ones with dimension [dx1]. The expressions on the right and left of the RHS can be computed efficiently in O(NxP) and O(PxK), but the computation of the term in the middle is O(NxPxK) which is the bottleneck. In Multinomial Mixture, instead of the cluster means we have class-probabilities in matrix M. In this case, the distance measure is simply the log-probability of the instance given a class i.e. Xxlog(M) which is again matrix product.
So, how do we make ML implementations faster? Matrix multiplication seems like it should be a very well studied topic and all that remains is to choose an efficient matrix multiplication library and plug it in. Unfortunately, 'choosing' the right library turned out to be a much harder problem than I thought. There are tons of implementations of the BLAS interface and each has a different implementation of the matrix multiplication function (see DGEMM function).
I performed a series of dense-dense matrix multiplication experiments on 5 BLAS implementations - ATLAS, EIGEN matrix template library, Intel's Math Kernel Library (MKL), OpenBLAS, and AMD's core Math Library (ACML) so that I could choose the 'right' library. Note that MATLAB internally uses Intel's MKL library although with some overhead.
All the tests were performed on 48 core and 66GB RAM machine with configuration given here.
Preliminaries
- ATLAS: The entire ATLAS source-code was recompiled on the target machine (with the appropriate tuning). Unfortunately, I could not deselect cpu-throttling; but I doubt if that would make too much difference in performance.
I Compiled two versions - one with multithreading and one without. Since it is not possible to control the number of threads in the multithreaded version without recompiling from scratch, I could run ATLAS either with #cores=1 or #cores=48. - EIGEN: The library is only header files. Defined EIGEN_NO_DEBUG to prevent run-time assertions. The single-threaded version was compiled using -DEIGEN_DONT_PARALLELIZE. Obviously, I used EIGEN's native BLAS implementation and did not link it to MKL.
- MKL: The multi-threaded version was linked to mkl_gnu_thread (and not mkl_intel_thread) and the single-threaded version was linked to mkl_sequential_thread.
- ACML: Since ACML is not compatible with gcc, I used Open64 compiler to compile the program.
- OpenBLAS: The OpenBLAS source-code was recompiled on the target machine to perform appropriate tuning. Unfortunately, there is no native single-threaded version of OpenBLAS. I mimicked the single-threaded version by setting OMP_NUM_THREADS=1, note that this could 'potentially' lead to slightly lower performance.
Single Core Timing
I performed a sequence of matrix multiplications on squared matrices with increasingly larger dimensions. The time-taken for each BLAS implementation is reported (averaged over 5 runs) is shown below,
| Matrix-Dimension | ATLAS | EIGEN | MKL | OpenBLAS | ACML |
|---|---|---|---|---|---|
| 500 | 0.039407 | 0.049505 | 0.037311 | 0.03636 | 0.03682 |
| 1000 | 0.306288 | 0.367053 | 0.293855 | 0.284742 | 0.28739 |
| 1500 | 1.025238 | 1.236386 | 0.987354 | 0.954938 | 0.960183 |
| 2000 | 2.411613 | 2.885663 | 2.338211 | 2.252574 | 2.261928 |
| 2500 | 4.706949 | 5.714484 | 4.560049 | 4.410473 | 4.404316 |
| 3000 | 8.132255 | 9.766208 | 7.857467 | 7.585038 | 7.586482 |
| 3500 | 12.907831 | 15.584621 | 12.511223 | 12.068317 | 12.029348 |
| 4000 | 19.239628 | 22.97125 | 18.623505 | 17.991189 | 17.918091 |
| 4500 | 27.431941 | 33.32037 | 26.500993 | 25.615759 | 25.623473 |
| 5000 | 37.628072 | 44.882824 | 36.376913 | 35.246075 | 35.053436 |
After a few lines of R,
dat = read.table("core1.dat",
header = TRUE,
row.names = "Matrix-Dimension",
check.names = FALSE);
png("core1.png" , width=800 , height=500 );
par(mar=c(5,5,2,2));
barplot(t(as.matrix(dat)),
beside = TRUE,
col = c("LightBlue","DeepSkyBlue","SteelBlue",
"MediumBlue","MidnightBlue") ,
xlab="Matrix Dimension" ,
ylab="Time (secs)" ,
cex.lab=1.5 ,
cex.axis=1.5 ,
ylim=c(0,45));
legend("topleft",
names(dat),
cex = 1.3,
bty = "n",
fill = c("LightBlue","DeepSkyBlue","SteelBlue",
"MediumBlue","MidnightBlue") );
dev.off();
We have a nice graph (lower the time, better)
OpenBLAS giving the best speed is a surprise, I would've expected ACML to win hands down because I am testing on a AMD machine. Also, it seems like I am getting contrary results to EIGEN's benchmark - EIGEN performs pretty badly, it just does not scale to larger matrices. But apart from EIGEN, there does not seem to be human-noticeable difference between OpenBLAS and ACML and MKL.
Multi Core Timing
In this setting, the implementations are allowed to use multiple cores to perform the matrix-multiplication task. All results are averaged over 5 runs. I show the timing comparisons for number of cores=8, 32 and 48.
#CORES = 8
| Matrix-Dimension | EIGEN | MKL | OpenBLAS | ACML |
|---|---|---|---|---|
| 1000 | 0.065014 | 0.043362 | 0.037348 | 0.308233 |
| 2000 | 0.400732 | 0.326562 | 0.295117 | 2.356271 |
| 3000 | 1.394491 | 1.075646 | 0.984161 | 7.846398 |
| 4000 | 3.136368 | 2.51627 | 2.330076 | 18.471795 |
| 5000 | 5.844691 | 4.874892 | 4.522203 | 35.977965 |
| 6000 | 10.712579 | 8.3478 | 7.795672 | 61.851248 |
| 7000 | 16.625342 | 13.215622 | 12.402947 | 97.811272 |
| 8000 | 25.063683 | 19.603807 | 18.362227 | 145.382045 |
| 9000 | 34.53994 | 28.013694 | 26.256471 | 208.371312 |
| 10000 | 46.942471 | 38.141061 | 36.120998 | 286.216164 |
#CORES = 32
| Matrix-Dimension | EIGEN | MKL | OpenBLAS | ACML |
|---|---|---|---|---|
| 1000 | 0.023529 | 0.016461 | 0.01041 | 0.351531 |
| 2000 | 0.416129 | 0.112076 | 0.077994 | 2.515941 |
| 3000 | 0.944631 | 0.362674 | 0.261565 | 8.27491 |
| 4000 | 1.751315 | 0.711094 | 0.621344 | 19.235383 |
| 5000 | 2.81821 | 1.321439 | 1.186354 | 37.563696 |
| 6000 | 4.270897 | 2.288235 | 2.0397 | 64.253479 |
| 7000 | 6.060917 | 3.511501 | 3.23041 | 101.239577 |
| 8000 | 8.294816 | 5.135532 | 4.790252 | 150.489878 |
| 9000 | 10.775887 | 7.25866 | 6.914698 | 217.521048 |
| 10000 | 14.333916 | 9.942657 | 9.327124 | 295.003328 |
#CORES = 48
| Matrix-Dimension | ATLAS | EIGEN | MKL | OpenBLAS | ACML |
|---|---|---|---|---|---|
| 1000 | 0.043054 | 0.024524 | 0.017696 | 0.007697 | 0.381892 |
| 2000 | 0.133291 | 0.201383 | 0.136436 | 0.054589 | 2.639059 |
| 3000 | 0.355704 | 1.272564 | 0.433831 | 0.182858 | 8.563053 |
| 4000 | 0.799005 | 1.51747 | 1.009579 | 0.484006 | 19.069397 |
| 5000 | 1.509474 | 1.217192 | 1.018603 | 0.831552 | 38.072026 |
| 6000 | 2.317285 | 5.054719 | 1.589423 | 1.443241 | 65.568967 |
| 7000 | 3.727477 | 4.677896 | 2.628318 | 2.240029 | 102.94063 |
| 8000 | 6.116075 | 12.265269 | 3.801652 | 3.383855 | 152.98614 |
| 9000 | 8.611308 | 11.833728 | 5.121538 | 4.719928 | 221.550268 |
| 10000 | 10.627788 | 10.495585 | 6.896077 | 6.657801 | 299.49296 |
ACML is out of the window when it comes to multithreaded BLAS - the timings were so bad that I could not even plot (did I make a mistake ?). OpenBLAS seems to offer the best performance closely followed by MKL. Despite the slower performance than MKL, ATLAS still seems to do better than EIGEN.
Scaling
I tested the how the speed of each implementation increases as the number of cores increases. The next two graphs shows the time-taken and speedup achieved on a 5000x5000 matrix multiplication by slowly increasing the number of cores from 1 to 48 (results are again averaged over 5 runs). I do not show the results of ACML and ATLAS - ACML is slow, and ATLAS cannot dynamically change the number of threads.
OpenBLAS is the only implementation that can successfully make use of any additional cores. The results of EIGEN and MKL are jagged - so that means that sometimes increasing the number of cores can hurt the performance for EIGEN and MKL. Although counter-intuitive, a closer inspection reveals that the optimal number of cores for MKL is when it is a multiple of 4. The performance of MKL reduces/not improve if the number of cores is not a multiple of 4 - this is something to note. I could not find a similar pattern for EIGEN though.
An equally informative though popularly used metric is Speed Up (how much faster is the multi-threaded version compared to a single-threaded one).
The dotted red line shows the optimal performance with perfect parallelization. OpenBLAS does come pretty close to that.
CONCLUSION
OpenBLAS seems to be the best library (atleast w.r.t to the machine I ran the tests on) for Dense-Dense matrix multiplication. It scales well with increasing number of cores as well as increasing size of matrices .
For multi-threaded applications,
OpenBLAS > MKL > ATLAS >> EIGEN > ACML
For single-threaded applications,
OpenBLAS ≈ ACML > MKL > ATLAS >> EIGEN
May be next-time I will post some of the comparisons on Sparse-Dense matrix multiplication,
SOURCE CODE
I've attached the source-code for the programs and the plotting scripts here as well as at github





This comment has been removed by the author.
ReplyDeleteI ran similar tests many many years ago (GotoBLAS times), with similar results. Except MKL really shone above all others in single precision operations, for some reason.
ReplyDeleteWould be interesting to see the benchmarks on single precision (sgemm) too.
(the link to configuration file says "No content to display" btw)
What Eigen loses in speed, it gains in being a whole vector-matrix package, though, with lots of native C++ goodness.
ReplyDeleteHard Rock Hotel & Casino Toledo - MapyRO
ReplyDeleteHard 의왕 출장샵 Rock Hotel & Casino Toledo is a 4-star hotel with a restaurant, bars, spa, live 하남 출장안마 entertainment and 청주 출장샵 a 포항 출장안마 casino. View detailed floor plans, amenities, 사천 출장마사지 photos,